Дистилляция
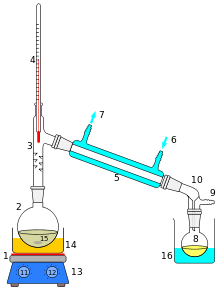
Устройство перегонного аппарата.
1 Нагревательный элемент
2 Перегонный куб
3 Насадка Вюрца/каплеуловитель
4 Термометр
5 Холодильник
6 Подвод охлаждающей жидкости
7 Отвод охлаждающей жидкости
8 Приёмная колба
9 Отвод газа (в том числе с понижением давления)
10 Аллонж
11 Регулятор температуры нагревателя
12 Регулятор скорости перемешивания
13 Магнитная мешалка
14 Водяная (масляная, песочная и т. п.) баня
15 Мешалка или центры кипения
16 Охлаждающая ванна
Дистилля́ция (лат. distillatio — стекание каплями[1]) — перегонка, испарение жидкости с последующим охлаждением и конденсацией паров.
Дистилляцию рассматривают прежде всего как технологический процесс разделения и рафинирования многокомпонентных веществ — в ряду других процессов с фазовым превращением и массообменом: сублимация, кристаллизация, жидкостная экстракция и некоторых других. Различают дистилляцию с конденсацией пара в жидкость (при которой получаемый дистиллят имеет усреднённый состав вследствие перемешивания) и дистилляцию с конденсацией пара в твёрдую фазу (при которой в конденсате возникает распределение концентрации компонентов). Продуктом дистилляции является дистиллят или остаток (или и то, и другое) — в зависимости от дистиллируемого вещества и целей процесса. Основными деталями дистилляционного устройства являются обогреваемый контейнер (куб) для дистиллируемой жидкости, охлаждаемый конденсатор (холодильник) и соединяющий их обогреваемый паропровод.
Содержание
1 История
2 Применение
3 Теория дистилляции
4 Дистилляция с конденсацией пара в жидкость
5 Дистилляция с конденсацией пара в твёрдую фазу
6 Экстрактивная дистилляция (дистилляция с добавочным компонентом)
7 См. также
8 Примечания
9 Литература
История |
Первые сведения о дистилляции относятся к I веку и упоминаются в работах греческих алхимиков в Александрии (Египет)[2]. В XI веке, у Авиценны, дистилляция упоминается как метод получения эфирных масел. C середины XIX века разрабатывается ректификация.
Применение |
Дистилляция применяется в промышленности и в лабораторной практике для разделения и рафинирования сложных веществ: для разделения смесей органических веществ (например, разделение нефти на бензин, керосин, дизельное топливо и др.; получение душистых веществ в парфюмерии; очистка этилового спирта) и для получения высокочистых неорганических веществ (например, металлов: бериллия, свинца, цинка, магния, кадмия, ртути; и неметаллов: серы, селена и др.).
Теория дистилляции |
В теории дистилляции в первую очередь рассматривается разделение смесей двух веществ[1]. Принцип дистилляции основан на том, что концентрация C1{displaystyle C_{1}}




Режимы дистилляции характеризуются температурой испарения и степенью отклонения от фазового равновесия жидкость-пар. Обычно в дистилляционном процессе n=n1+nc{displaystyle n=n_{1}+n_{c}}






Идеальный коэффициент разделения двухкомпонентного вещества может быть выражен через давления p10{displaystyle p_{1}^{0}}





При nc=n{displaystyle n_{c}=n}











Для различных режимов дистилляции выведены уравнения, связывающие содержание второго компонента в конденсате C/C0{displaystyle C/C_{0}}








При дистилляции вещества с большой концентрацией компонентов с конденсацией пара в жидкость при несильной зависимости коэффициентов активности компонентов от их концентраций взаимосвязь величин G1/G0{displaystyle G_{1}/G_{0}}


- lgG1G0=1β−1lgC1C0−ββ−1lg100−C1100−C0.{displaystyle operatorname {lg} {tfrac {G_{1}}{G_{0}}}={tfrac {1}{beta -1}}operatorname {lg} {tfrac {C_{1}}{C_{0}}}-{tfrac {beta }{beta -1}}operatorname {lg} {tfrac {100-C_{1}}{100-C_{0}}}.}
Для дистилляции с конденсацией пара в жидкость при малом содержании примеси
- C/C0=1−(1−G/G0)βG/G0,{displaystyle C/C_{0}={tfrac {1-(1-G/G_{0})^{beta }}{G/G_{0}}},}
C1/C0{displaystyle C_{1}/C_{0}}=(G1/G0)β−1,{displaystyle (G_{1}/G_{0})^{beta -1},}
где β{displaystyle beta }
Приведённые дистилляционные уравнения описывают не только процессы равновесия компонентов в системах газ-жидкость, но и при описании распределения компонентов двух контактирующих фаз при интенсивном перемешивании (например, переходы жидкий кристалл-кристалл, жидкий кристалл-жидкость, газ-плазма, а также в переходах, связанных с квантово-механическими состояниями — сверхтекучая жидкость, конденсат Бозе — Эйнштейна) — при подстановке в них соответствующих коэффициентов разделения. Зачастую они пригодны для теоретического описания сублимации — прежде всего, при температуре вблизи температуры плавления.
Дистилляция с конденсацией пара в жидкость |
Простая перегонка — частичное испарение жидкой смеси путём непрерывного отвода и конденсации образовавшихся паров в холодильнике. Полученный конденсат называется дистиллятом, а неиспарившаяся жидкость — кубовым остатком.
Фракционная дистилляция (или дробная перегонка) — разделение многокомпонентных жидких смесей на отличающиеся по составу части, фракции, путём сбора конденсата частями с различной летучестью, начиная с первой, обогащенной низкокипящим компонентом. Остаток жидкости обогащён высококипящим компонентом. Для улучшения разделения фракций применяют дефлегматор.
Ректификация — способ дистилляции, при котором часть жидкого конденсата (флегма) постоянно возвращается в куб, двигаясь навстречу пару в колонне. В результате этого примеси, содержащиеся в паре, частично переходят во флегму и возвращаются в куб, при этом чистота пара (и конденсата) повышается.
Дистилляция с конденсацией пара в твёрдую фазу |
Дистилляция с конденсацией пара в градиенте температуры — дистилляционный процесс, в котором конденсация в твёрдую фазу осуществляется на поверхности, имеющей градиент температуры, с многократным реиспарением частиц пара. Менее летучие компоненты осаждаются при более высоких температурах. В результате в конденсате возникает распределение примесей вдоль температурного градиента, и наиболее чистая часть конденсата может быть выделена в качестве продукта. Разделение компонентов пара при реиспарении подчиняется собственным закономерностям. Так, при молекулярной дистилляции соотношение между количествами Q1{displaystyle Q_{1}}

- Q1/Q2=(μη1W10−W1)/(μη2W20−W2),{displaystyle Q_{1}/Q_{2}=(mu eta _{1}W_{1}^{0}-W_{1})/(mu eta _{2}W_{2}^{0}-W_{2}),}
где W10{displaystyle W_{1}^{0}}






Этот вид дистилляции нашёл применение в промышленном производстве высокочистого бериллия.
Дистилляция с направленным затвердеванием конденсата (дистилляция с вытягиванием дистиллята) — дистилляционный процесс в контейнере удлинённой формы c полным расплавлением дистиллируемого вещества и конденсацией пара в твёрдую фазу по мере вытягивания конденсата в холодную область. Процесс разработан теоретически.
В получаемом конденсате возникает неравномерное распределение примесей, и наиболее чистая часть конденсата может быть выделена в качестве продукта. Процесс является дистилляционным аналогом нормальной направленной кристаллизации. Распределение примеси в конденсате описывается уравнением:
- C/C0=β(1−x/L)β−1,{displaystyle C/C_{0}=beta (1-x/L)^{beta -1},}
где C{displaystyle C}


Зонная дистилляция — дистилляционный процесс в контейнере удлинённой формы c частичным расплавлением рафинируемого вещества в перемещаемой жидкой зоне и конденсацией пара в твёрдую фазу по мере выхода конденсата в холодную область. Процесс разработан теоретически.
При движении зонного нагревателя вдоль контейнера сверху вниз в контейнере формируется твёрдый конденсат с неравномерным распределением примесей, и наиболее чистая часть конденсата может быть выделена в качестве продукта. Процесс может быть повторён многократно, для чего конденсат, полученный в предыдущем процессе, должен быть перемещён (без переворота) в нижнюю часть контейнера на место рафинируемого вещества. Неравномерность распределения примесей в конденсате (то есть эффективность очистки) растёт с увеличением числа повторений процесса.
Зонная дистилляция является дистилляционным аналогом зонной перекристаллизации. Распределение примесей в конденсате описывается известными уравнениями зонной перекристаллизации с заданным числом проходов зоны — при замене коэффициента распределения k{displaystyle k}

C/C0=1−(1−β)exp(−β{displaystyle C/C_{0}=1-(1-beta )exp(-beta }x/λ),{displaystyle x/lambda ),}
где C{displaystyle C}


Экстрактивная дистилляция (дистилляция с добавочным компонентом) |
Эффективность дистилляционной очистки может быть повышена введением в систему основа-примесь добавочного компонента (обычно в концентрации 0,5…10 %), который изменяет относительную летучесть примеси. Разновидностью метода является дистилляция в атмосфере активного вещества, прежде всего — водяного пара.
См. также |
- Дефлегмация
- Ректификация
- Ректификационная колонна
- Дистилляция термокомпрессионная
- Экстрактивная дистилляция
Примечания |
↑ 12 Дистилляция / В. Л. Пебалк // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Forbes, Robert James. A short history of the art of distillation: from the beginnings up to the death of Cellier Blumenthal. — BRILL, 1970. — ISBN 978-90-04-00617-1.
Литература |
Дытнерский Ю. И. Процессы и аппараты химической технологии: Учебник для вузов. Изд. 2. В 2-х кн. Часть 2. Массообменные процессы и аппараты. М.: Химия, 1995. — 368 с.
Гельперин Н. И. Основные процессы и аппараты химической технологии. — М.: Химия, 1981. — 812 с.
Девятых Г. Г., Еллиев Ю. Е. Введение в теорию глубокой очистки веществ. — М.: Наука, 1981. — 320 с.
Девятых Г. Г., Еллиев Ю. Е. Глубокая очистка веществ. — М.: Высшая школа, 1990. — 192 с.
Емельянов В. С., Евстюхин А. И., Шулов В. А. Теория процессов получения чистых металлов, сплавов и интерметаллидов. — М.: Энергоатомиздат, 1983. — 144 с.
Жаров В. Т., Серафимов Л. А. Физико-химические основы дистилляции и ректификации. — Л.: Химия, 1975. — 240 с.
Степин Б. Д., Горштейн И. Г., Блюм Г. З., Курдюмов Г. М., Оглоблина И. П. Методы получения особо чистых неорганических веществ. — Л.: Химия, 1969. — 480 с.
Сийрде Э. К., Теаро Э. Н., Миккал В. Я. Дистилляция. — Л.: Химия, 1971. — 216 с.
Калашник О. Н., Нисельсон Л. А. Очистка простых веществ дистилляцией с гидротермальным окислением примесей // Высокочистые вещества, 1987. — № 2. — С. 74—78.
Корякин Ю. В., Ангелов И. И. Чистые химические вещества. Руководство по приготовлению неорганических реактивов и препаратов в лабораторных условиях. — М.: Химия, 1974.
Беляев А. И. Физико-химические основы очистки металлов и полупроводниковых веществ. — М.: Металлургия, 1973. — 224 с.
Нисельсон Л. А., Лапин Н. В., Бежок В. С. Определение относительных летучестей примесей в жидком германии // Высокочистые вещества, 1989. — N. 6. — С. 33—38 [Содержатся сведения о коэффициенте f скорости испарения вещества — со ссылкой на: Borrows G. // Trans. Inst. Chem. Eng., 1954. — V. 32. — P. 23.]
Пазухин В. А., Фишер А. Я. Разделение и рафинирование металлов в вакууме. — М.: Металлургия, 1969. — 204 с.
Иванов В. Е., Папиров И. И., Тихинский Г. Ф., Амоненко В. М. Чистые и сверхчистые металлы (получение методом дистилляции в вакууме). — М.: Металлургия, 1965. — 263 с.
Несмеянов А. Н. Давление пара химических элементов. — М.: Издательство АН СССР, 1961. — 320 с.
Есютин В. С., Нургалиев Д. Н. Вакуум-дистилляционная очистка свинца от примесей в аппарате непрерывного действия // Цветные металлы, 1975. — № 12. — С. 28-30.
Кравченко А. И. О временной зависимости состава двойного сплава при его разгонке в вакууме // Известия АН СССР. Серия: Металлы. — 1983. — № 3. — С. 61—63.
Кравченко А. И. Об уравнениях дистилляции при малом содержании примеси // Вопросы атомной науки и техники, 1990. — № 1 — Серия: «Ядерно-физические исследования» (9). — С. 29—30.
Нисельсон Л. Я., Ярошевский А. Г. Межфазовые коэффициенты распределения (Равновесия кристалл-жидкость и жидкость-пар). — М.: Наука, 1992. — 399 с.
Kravchenko A.I. Simple substances refining: efficiency of distillation methods // Functional Materials, 2000 — V. 7. — N. 2. — P. 315—318.
Кравченко А. И. Уравнение распределения примеси в твёрдом дистилляте // Неорганические материалы, 2007. — Т. 43. — № 8. — С. 1021—1022.
Кравченко А. И. Эффективность очистки в дистилляционном и кристаллизационном процессах // Неорганические материалы, 2010. — Т. 46. — № 1. — С. 99—101.
Кравченко А. И. Дистилляция с вытягиванием дистиллята // Вопросы атомной науки и техники, 2008. — № 1 — Серия: «Вакуум, чистые материалы, сверхпроводники» (17). — С. 18—19. [1]
Кравченко А. И. Зонная дистилляция // Вопросы атомной науки и техники, 2011. — № 6 — Серия: «Вакуум, чистые материалы, сверхпроводники» (19). — С. 24—26. [2]
Кравченко А. И. Разработка перспективных схем зонной дистилляции // Перспективные материалы, 2014. — № 7. — С. 68-72. [www.j-pm.ru].
Кравченко А. И. О распределении примесей при фазовых переходах из фазы с идеальным перемешиванием // Вопросы атомной науки и техники, 2011. — № 6 — Серия: «Вакуум, чистые материалы, сверхпроводники» (19). — С. 27—29. [3]
Кравченко А. И. Зависимость эффективного коэффициента разделения в некоторых металлических системах основа-примесь от степени перегонки // Неорганические материалы, 2015. — Т. 51. — № 2. — С. 146—147.
Папиров И. И., Кравченко А. И., Мазин А. И., Шиян А. В., Вирич В. Д. Распределение примесей в сублимате магния // Неорганические материалы, 2015. — Т. 51. — № 6. — С. 625—627.
Кириллов Ю. П., Кузнецов Л. А., Шапошников В. А. , Чурбанов М. Ф. Влияние диффузии на глубину очистки веществ дистилляцией // Неорганические материалы, 2015. — Т. 51. — № 11. — С. 1177—1189.
Кравченко А. И. Соотношение между эффективным и идеальным коэффициентами разделения при дистилляции и сублимации // Неорганические материалы, 2016. — Т. 52. — № 4. — С. 423—430.
Кириллов Ю. П., Шапошников В. А. , Кузнецов Л. А., Ширяев В. С. , Чурбанов М. Ф. Моделирование испарения жидких веществ и конденсации их паров при дистилляции // Неорганические материалы, 2016. — Т. 52. — № 11. — С. 1256—1261.
Кравченко А. И. О температурной зависимости идеального коэффициента разделения в системах с близкой летучестью компонентов // Вопросы атомной науки и техники, 2016. — № 1 — Серия: «Вакуум, чистые материалы, сверхпроводники» (21). — С. 14—16.
Папиров И. И., Кравченко А. И., Мазин А. И., Шиян А. В., Вирич В. Д. Распределения примесей в сублиматах магния // Вопросы атомной науки и техники, 2016. — № 1 — Серия: «Вакуум, чистые материалы, сверхпроводники» (21). — С. 21—22.
Жуков А. И., Кравченко А. И. Расчёт сублимации с учётом диффузии примеси // Неорганические материалы, 2017. — Т. 53. — № 6. — С. 662—668.
Кравченко А. И. О применимости идеального коэффициента разделения для расчёта дистилляции и сублимации // Вопросы атомной науки и техники, 2018. — № 1 — Серия: «Вакуум, чистые материалы, сверхпроводники» (22). — С. 14-17.
Кравченко А. И. О рафинировании простых веществ дистилляцией с добавочным компонентом // Вопросы атомной науки и техники, 2018. — № 1 — Серия: «Вакуум, чистые материалы, сверхпроводники» (22). — С. 9—13.
Кравченко А. И. Расчёт дистилляционного рафинирования вещества с легколетучей и труднолетучей примесями // Неорганические материалы, 2018. — Т. 54. — № 5. — С. 520—522.- ГОСТ 2177—99 (ASTM D86). Нефтепродукты. Методы определения фракционного состава
Для улучшения этой статьи желательно: |