Волна
Волна́ — изменение некоторой совокупности физических величин (характеристик некоторого физического поля или материальной среды), которое способно перемещаться, удаляясь от места его возникновения, или колебаться внутри ограниченных областей пространства[1].
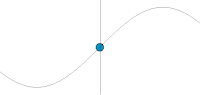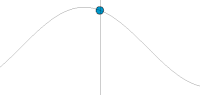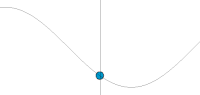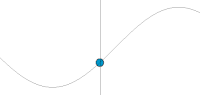
Графическое представление гармонического колебания и волны.
По горизонтальной оси отложена координата пространства, по вертикальной — значение физической величины в каждый текущий момент времени. Чтобы показать, как физическая величина зависит сразу от двух переменных (пространства и времени), картинка сделана анимированной.
Видно, что в каждой отдельно взятой точке пространства (например, в центре картинки) значение физической величины изменяется во времени, в каждой отдельно взятой точке пространства происходит колебание физической величины.
Однако совокупность колебаний в соседних точках пространства происходит не случайно, а особым образом, так, что в соседних кадрах анимированной картинки (в каждый последующий момент времени) график пространственной зависимости физической величины (серая линия) совпадает с самим собой, отличаясь только сдвигом вправо (удовлетворяет волновому уравнению). Именно такое поведение физической величины в пространстве и во времени называют волной. В данном примере это бегущая волна с гармонической временной зависимостью, распространяющаяся в однородной среде без потерь в направлении слева направо
Волновой процесс может иметь самую разную физическую природу: механическую, химическую (реакция Белоусова — Жаботинского, протекающая в автоколебательном режиме каталитического окисления различных восстановителей бромисто-водородной кислотой HBrO3), электромагнитную (электромагнитное излучение), гравитационную (гравитационные волны), спиновую (магнон), плотности вероятности (ток вероятности) и т. д. Как правило, распространение волны сопровождается переносом энергии, но не переносом массы.
Многообразие волновых процессов приводит к тому, что никаких абсолютных общих свойств волн выделить не удаётся[1]. Одним из часто встречающихся признаков волн считается близкодействие, проявляющееся во взаимосвязи возмущений в соседних точках среды или поля, однако в общем случае[уточнить] может отсутствовать и оно[1].
Среди всего многообразия волн выделяют некоторые их простейшие типы, которые возникают во многих физических ситуациях из-за математического сходства описывающих их физических законов[1]. Об этих законах говорят в таком случае как о волновых уравнениях. Для непрерывных систем это обычно дифференциальные уравнения в частных производных в фазовом пространстве системы, для сред часто сводимые к уравнениям, связывающим возмущения в соседних точках через пространственные и временные производные этих возмущений[1]. Важным частным случаем волн являются линейные волны, для которых справедлив принцип суперпозиции.
В основном физические волны не переносят материю, но возможен вариант, где происходит волновой перенос именно материи, а не только энергии. Такие волны способны распространяться сквозь абсолютную пустоту. Примером таких волн может служить нестационарное излучение газа в вакуум, волны вероятности электрона и других частиц, волны горения, волны химической реакции, волны плотности реагентов / транспортных потоков[источник не указан 1809 дней].
Содержание
1 Происхождение волн
2 Характеристики волн
2.1 Геометрические элементы
2.2 Временна́я и пространственная периодичности
2.3 Интенсивность волны
3 Классификации волн
3.1 Влияние субстанции
3.2 По отношению к направлению колебаний частиц среды
3.3 По геометрии фронта волны (поверхности равных фаз)
3.4 По математическому описанию
3.5 По времени возбуждения субстанции
4 Общие свойства волн
4.1 Резонансные явления
4.2 Распространение в однородных средах
4.3 Дисперсия
4.4 Поляризация
4.5 Взаимодействие с телами и границами раздела сред
4.6 Наложение волн
5 Математические выражения, описывающие волновые процессы
5.1 Гармоническая волна
5.2 Лучи волны
6 Направления исследований волн
7 См. также
8 Примечания
9 Литература
10 Ссылки
Происхождение волн |
Волны могут генерироваться различными способами.
- Генерация локализованным источником колебаний (излучателем, антенной).
- Спонтанная генерация волн в объёме при возникновении гидродинамических неустойчивостей. Такую природу могут иметь, например, волны на воде при достаточно большой скорости ветра, дующего над водной гладью.
- Переход волн одного типа в волны другого типа. Например, при распространении электромагнитных волн в кристаллическом твёрдом теле могут генерироваться звуковые волны.
Характеристики волн |
Базовым представителем волн являются линейные распространяющиеся волны, возникающие в системах, динамика которых может быть описана линейными гиперболическими уравнениями второго порядка (волновыми уравнениями) относительно характеристик системы Ψi{displaystyle Psi _{i}}
- ∂2Ψi∂t2−∑j,kAi,kj∂2Ψj∂xk2=0,{displaystyle {frac {partial ^{2}Psi _{i}}{partial t^{2}}}-sum _{j,k}A_{i,k}^{j}{frac {partial ^{2}Psi _{j}}{partial x_{k}^{2}}}=0,}
где матрицы Ai,kj{displaystyle A_{i,k}^{j}}

Геометрические элементы |
Геометрически у волны выделяют следующие элементы:
гребень волны — множество точек волны с максимальным положительным отклонением от состояния равновесия;
долина (ложбина) волны — множество точек волны с наибольшим отрицательным отклонением от состояния равновесия;
волновая поверхность — множество точек, имеющих в некий фиксированный момент времени одинаковую фазу колебаний. В зависимости от формы фронта волны выделяют плоские, сферические, эллиптические и другие волны.
Терминология гребня и ложбины волны, как правило, применима к поверхностным волнам на границе двух сред — например, для поверхностных волн на воде. Иногда эту терминологию используют для описания графиков волнового процесса. Для продольных волн используются понятия экстремальных точек волны: точек максимального сжатия и максимального разрежения[2]. При этом в случае механических волн соответствующие элементарные объёмы смещаются из своих положений равновесия к области максимального сжатия или от области максимального разрежения с обеих сторон от волновых поверхностей, проходящих через экстремальные точки волны. Максимума же или минимума достигают только параметры субстанции — например, давление в элементарном объёме, концентрация определённого химического вещества, напряжённость поля, плотность элементов дискретной динамической системы и т. д.
Для стоячих волн используют понятие пучность и узел.
Временна́я и пространственная периодичности |
Поскольку волновые процессы обусловлены совместным колебанием элементов динамической системы (осцилляторов, элементарных объёмов), они обладают как свойствами колебаний своих элементов, так и свойствами совокупности этих колебаний.
К первым относится временная периодичность — период T повторения колебаний волнового процесса в некоторой точке пространства,
T=1/f,{displaystyle T=1/f,}
где f{displaystyle f}

Ко вторым относится пространственная периодичность — длина волны λ, равная пространственному периоду волнового процесса в окрестности некоторой точки пространства в некоторый момент времени, связанная с волновым числом k= 2π/λ [радиан/м] — скоростью изменения фазы волнового процесса с изменением координаты, «пространственной круговой частотой».
Временная и пространственная периодичности взаимосвязаны. В упрощённом виде для линейных волн эта зависимость имеет следующий вид[3]:
f=c/λ,{displaystyle f=c/lambda ,}
где c — скорость распространения волны в данной среде.
Для сложных процессов с дисперсией и нелинейностью, данная зависимость применима для каждой частоты спектра, в который может быть разложен любой волновой процесс.
Интенсивность волны |
Для характеристики интенсивности волнового процесса используют три параметра: амплитуда волнового процесса, плотность энергии волнового процесса и плотность потока энергии (плотность потока мощности).
Классификации волн |
Имеется множество классификаций волн, различающихся по своей физической природе, по конкретному механизму распространения, по среде распространения и т. п.
По своему характеру волны подразделяются на[источник не указан 2637 дней]:
- По признаку распространения в пространстве: стоячие, бегущие.
- По характеру волны: колебательные, уединённые (солитоны).
- По типу волн: поперечные, продольные, смешанного типа.
- По законам, описывающим волновой процесс: линейные, нелинейные.
- По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях.
- По геометрии: сферические (пространственные), одномерные (плоские), спиральные.
Бегущие волны, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»[источник не указан 2637 дней]).
Влияние субстанции |
Особенности физической среды, в которой распространяются волны, накладывают особенности на характер их распространения, оставляя неизменными базовые волновые свойства. В связи с этим различают следующие основные виды волн:
- Механические упругие волны в твёрдых, жидких, газообразных материалах:
Волны на границе двух сред (поверхностные волны);- Продольные волны в субстанции;
- Поперечные волны;
- Волны сдвиговой деформации;
- Компаундные волны, возникающие в результате суперпозиции продольных противофазных волн в средах без сдвиговой деформации (жидких, газообразных);
- Электромагнитные волны;
- Волновые процессы в проводящих средах, в том числе и волны в плазме;
Гравитационные волны.
По отношению к направлению колебаний частиц среды |
Продольные волны (волны сжатия, P-волны) — частицы среды колеблются параллельно (по) направлению распространения волны (как, например, в случае распространения звука);
Поперечные волны (волны сдвига, S-волны) — частицы среды колеблются перпендикулярно направлению распространения волны (волны на границах разделения сред, электромагнитные волны);- Волны смешанного типа.
По геометрии фронта волны (поверхности равных фаз) |
Плоская волна — плоскости равных фаз перпендикулярны направлению распространения волны и параллельны друг другу.
Сферическая волна — поверхностью равных фаз является сфера.
Цилиндрическая волна — поверхностью равных фаз является цилиндрическая поверхность.
Спиральная волна — образуется в случае, если сферический или цилиндрический источник или источники волны в процессе излучения движутся по некоторой замкнутой кривой.
| Продольные волны: | Поперечные волны: |
|---|---|
 а) плоская; | 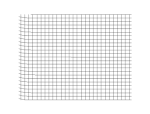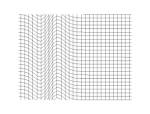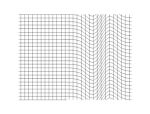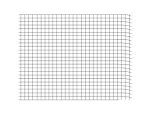 а) плоская; |
 б) сферическая. |  б) спиральная. |
По математическому описанию |
- Линейные волны — волны с небольшой амплитудой, свойства которых описываются стандартным волновым уравнением для идеальной субстанции;
Нелинейные волны — волны с большими амплитудами, что приводит к возникновению совершенно новых эффектов и существенно изменяет характер уже известных явлений. К ним, в частности, относят:
- Волны в средах с нелинейными параметрами, изменяющимися со степенью возмущения среды, волны в неоднородных средах;
Солитоны (уединённые волны);
Ударные волны сопровождающиеся нормальными разрывами.
Часто к нелинейным волнам относят поверхностные волны, сопутствующие продольным волнам в ограниченном объёме сплошной среды. В действительности эффект возникает в связи со смещённым на π{displaystyle pi }
Также часто к нелинейным относят некоторые типы наклонных волн. Тем не менее, в ряде случаев, как например при возбуждении поверхностных волн источником продольных волн, расположенным на дне объёма, или при возбуждении колебаний в стержнях под действием наклонной силы, — наклонные волны возникают при синфазном наложении. Описываются эти типы волн линейным волновым уравнением.
Также как в случае распространения волн в средах с изломом при анизотропности параметров среды для продольных и поперечных волн, наклонные волны тоже описываются линейными уравнениями, хотя их решения показывают даже срыв колебательного процесса на изломе. Их обычно относят к нелинейным колебательным процессам, хотя по сути они таковыми не являются.
Следует отметить, что в ряде случаев волновые процессы в линиях с сопротивлением могут быть сведены к решению линейного волнового уравнения (системы линейных волновых уравнений для дискретных динамических систем).
По времени возбуждения субстанции |
Монохроматическая волна — линейная волна с гармонической временной зависимостью от колебаний(то есть фурье-спектр которой отличен от нуля на единственной частоте), распространяющаяся в субстанции неопределённое (в математическом описании бесконечное или полубесконечное) время[4][5].
Одиночная волна — короткое одиночное возмущение (солитоны). Фурье-спектр такой волны является сплошным, то есть содержит бесконечное число гармонических волн.
Волновой пакет — последовательность возмущений, ограниченных во времени, с перерывами между ними. Одно беспрерывное возмущение такого ряда называется цугом волн. В теории волновой пакет описывается как сумма всевозможных плоских волн при периодичности последовательности образующих линейчатый спектр, взятых с определёнными весами. В случае нелинейных волн, форма огибающей волнового пакета может эволюционировать во времени и в пространстве, в котором распространяется волна. Для описания этих изменений используется автокорреляционная функция (АКФ), позволяющая судить о степени связи (корреляции) сигнала с его сдвинутой копией. Для дискретных динамических систем в ряде случаев амплитуды спектра могут быть найдены путём решения линейной системы уравнений для каждого члена ряда Фурье.
Общие свойства волн |
Резонансные явления |
В ограниченных в пространстве субстанциях волновым процессам свойственно проявление резонансных эффектов, обусловленных множественным наложением прямых и отражённых от границ волн, что приводит к резкому возрастанию амплитуды волнового процесса. При множественном наложении в области резонанса происходит аддитивное накопление энергии динамической системой вследствие синфазности прямых и обратных волн. Обычно принято считать, что в идеальных динамических системах без диссипации энергии при частоте резонанса амплитуда колебаний становится бесконечной, но это не всегда происходит, поскольку энергия свободных колебаний во многих случаях остаётся конечной.
Здесь следует различать особенности возникновения резонансов в динамических системах:
- Резонансные явления различаются в зависимости от того, являются ли волновые процессы вынужденными или свободными.
Вынужденные процессы возникают в системе при постоянном динамическом воздействии внешней силы. В этом случае спектр колебаний, возникающих в системе, является непрерывным с возрастанием амплитуды на резонансных частотах.
Расчетная амплитудно-частотная (а) и фазо-частотная (б) характеристики входного сопротивления Rin{displaystyle R_{in}}


На графиках мы видим, что при определенной нагрузке графики амплитуды и фазы становятся монотонными (красная линия), что свидетельствует об отсутствии отражения от конца линии, и линия ведёт себя как бесконечная.
Вынужденные волновые процессы описываются волновым уравнением (системой уравнений для динамических систем с сосредоточенными параметрами) с правой частью, в которую подставляется значение воздействующей внешней силы. В математике такого типа уравнения называются неоднородными, а их решения называют частными решениями[6]
Свободные колебания являются результатом последействия после окончания воздействия внешнего возмущения. Для этих волновых процессов характерен дискретный спектр, соответствующий частотам внутренних резонансов динамической системы. Данные колебания описываются волновым уравнением (системой уравнений) с нулевой правой частью. В математике такого типа дифференциальные уравнения называют однородными, а их решения — общими. Для нахождения постоянных интегрирования в данном случае требуется знание ненулевых параметров колебания хотя бы в одной точке динамической системы. При нулевом отклонении параметров всей системы (отсутствии предварительного возмущения) общее решение уравнения будет обращаться в ноль. При этом частное решение может быть и ненулевым. Таким образом, общее и частное решение волнового уравнения описывают различные процессы, возникающие в динамической системе. Частное решение описывает реакцию на непосредственное воздействие на систему, а общее решение — последействие системы при окончании воздействия на неё.
- Резонансные явления различаются в зависимости от дискретности или непрерывности самой динамической системы. В динамической системе с сосредоточенными параметрами резонансные явления даже в случае идеальности самой системы не приводят к бесконечному возрастанию амплитуды колебаний.
При предельном переходе к динамической системе с распределёнными параметрами в идеальном случае амплитуды возрастают до бесконечности. В линиях с сопротивлением, амплитуды резонансов в любом случае конечны. Величина сопротивления/вязкости влияет как на амплитуды резонансов, уменьшая их, так и смещает частоты резонансов.
- На резонансные явления оказывают влияние условия отражения волны на границах. Ранее мы видели, что при определённых условиях отражения от границы, конечная динамическая система ведёт себя как бесконечная. При неполном отражении от границы возникают совместные стоячие и прогрессивные волны, описываемые коэффициентом стоячей волны.
Если волновое сопротивление границы (в динамических системах с сосредоточенными параметрами) носит комплексный характер, то при определённых значениях такого сопротивления в динамической системе происходит резкое смещение резонансных частот.
Расчётная амплитудно-частотная (а) и фазо-частотная (b) характеристики входного сопротивления Rin{displaystyle R_{in}}


- На резонансные процессы влияют и свойства самой динамической системы. В частности, в дискретных динамических системах с резонансными подсистемами возникает четвёртый, резонансный тип колебаний, названный экспериментально открывшим его проф. Скучиком «колебания с отрицательной мерой инерции», поскольку при этих колебаниях входное сопротивление системы становится отрицательным. Это означает, что элемент, на который воздействует внешняя сила, движется встречно направлению воздействия последней. В этом режиме амплитуды колебаний даже в дискретных динамических системах обращаются в бесконечность, и резонансы возникают как выше, так и ниже частотного диапазона резонансов основной динамической системы.
Динамические системы с сосредоточенными параметрами можно рассматривать как динамические системы с распределёнными параметрами при условии:
aλ≪1π,{displaystyle {frac {a}{lambda }}ll {frac {1}{pi }},}

где a{displaystyle a}
- Наконец, на резонансные вынужденные колебания в динамической системе влияет точка приложения внешней силы. При определённом положении резонансы могут возникать только в части динамической системы.
Диаграммы вынужденных колебаний в конечной однородной упругой линии с незакрепленными концами при воздействии внешней силы на внутренние элементы линии.
Причём указанная особенность проявляется и в апериодическом режиме колебаний.
Распространение в однородных средах |
При распространении волн изменения их амплитуды и скорости в пространстве и появление дополнительных гармоник зависят от свойств анизотропности среды, сквозь которую проходят волны, границ, а также характера излучения источников волн.
Чаще волны в некоторой среде затухают, что связано с диссипативными процессами внутри среды. Но в случае некоторых специальным образом подготовленных метастабильных сред амплитуда волны может, наоборот, усиливаться (пример: генерация лазерного излучения). Наличие в среде резонансных подструктур обусловливает и появление кратковременного и длительного послесвечения.
На практике монохроматические волны встречаются очень редко. Максимально приближаются к монохроматическому излучение лазера, мазера, радиоантенны. Условием монохроматичности является удалённость области рассмотрения от переднего фронта волны, а также характер излучения источника. Если источник некогерентный, излучение состоит из наложения большого числа отрезков волн. Для описания когерентности сигнала вводится понятие время когерентности и длина когерентности[7].
Учитывая свойства субстанции, в которой распространяется излучение, а также сложный в общем случае спектр сигнала, вводится понятие фазовой и групповой скорости волны, то есть скорость «центра тяжести» волнового пакета.
Групповая и фазовая скорости совпадают только для линейных волн в средах без дисперсии. Для нелинейных волн групповая скорость может быть как больше, так и меньше фазовой скорости. Однако иногда принято считать, что когда речь идёт о скоростях, близких к скорости света, проявляется заведомое неравноправие между групповой и фазовой скоростями. Фазовая скорость не является ни скоростью движения материального объекта, ни скоростью передачи данных, поэтому она может превышать скорость света, не приводя при этом ни к каким нарушениям теории относительности. Вместе с тем, это немного не точно. Базовые постулаты теории относительности, как и теоретические построения на них, основываются на распространении света в пустоте, то есть в среде без дисперсии, в которой фазовая и групповая скорости одинаковы. В вакууме фазовая и групповая скорость распространения света одинаковы, в воздухе, воде и некоторых других средах разница между ними пренебрежимо мала и ею в большинстве случаев можно пренебрегать[8]. Поэтому если фазовая скорость в среде без дисперсии оказывается большей или меньшей скорости света, то такое же значение будет принимать и групповая скорость.
Групповая скорость характеризует скорость движения сгустка энергии, переносимой волновым пакетом, и потому в большинстве случаев не превышает скорость света. Также при распространении волны в метастабильной среде удаётся в определённых случаях добиться групповой скорости, превышающей скорость света в среде, как например при распространении света в сероуглероде.
Поскольку волна переносит энергию и импульс, то её можно использовать для передачи информации. При этом возникает вопрос о максимально возможной скорости передачи информации с помощью волн данного типа (чаще всего речь идёт об электромагнитных волнах). При этом скорость передачи информации никогда не может превышать скорости света в вакууме, что было подтверждено экспериментально даже для волн, в которых групповая скорость превышает скорость света в среде распространения.
Дисперсия |
Дисперсия возникает при наличии зависимости скорости распространения волны в среде от частоты этой волны, то есть если волновое число k=f(ω){displaystyle k=fleft(omega right)}


V=v−λ∂v∂λ.{displaystyle V=v-lambda {frac {partial v}{partial lambda }}.}

- При ∂v/∂λ=0{displaystyle partial v/partial lambda =0}
дисперсия отсутствует.
- При ∂v/∂λ>0{displaystyle partial v/partial lambda >0}
V<v{displaystyle V<v}
и показатель преломления среды с ростом частоты уменьшается, поскольку частная производная от фазовой скорости и частная производная от показателя преломления по длине волны связаны соотношением
∂v∂λ=−cn2∂n∂λ.{displaystyle {frac {partial v}{partial lambda }}=-{frac {c}{n^{2}}}{frac {partial n}{partial lambda }}.}

Эту зависимость называют нормальной дисперсией. Она проявляется при прохождении света через стёкла и другие прозрачные среды. В этом случае максимумы волн волнового пакета движутся быстрее огибающей. В результате в хвостовой части пакета за счёт сложения волн возникают новые максимумы, которые передвигаются вперёд и пропадают в его головной части.
- При ∂v/∂λ<0{displaystyle partial v/partial lambda <0}
V>v{displaystyle V>v}
. Показатель преломления возрастает. Эта зависимость характеризует аномальную дисперсию, проявляющуюся в областях спектра, где наблюдается интенсивное поглощение. В этом случае максимумы волн появляются в головной части пакета, перемещаются назад и исчезают в его хвосте. При аномальной дисперсии «если показатель преломления сильно изменяется с частотой (∂n/∂λ{displaystyle partial n/partial lambda }
достаточно велико), то может оказаться, что групповая скорость V{displaystyle V}
, формально вычисленная по существующей формуле Рэлея, будет больше скорости света в вакууме, что противоречит специальной теории относительности»[9]. Данная особенность проявляется при прохождении ультракоротких радиоволн через ионосферу[10].
Во всех случаях ненулевой дисперсии волновой пакет со временем расплывается[8]. Ещё одной особенностью волнового пакета является то, что он, как и волны, его образующие, обладает принципом суперпозиции при прохождении через другие волновые пакеты, а также в однородной среде движется прямолинейно. Он не может ускоряться, замедляться или отклоняться от прямолинейности своего распространения другими волновыми пакетами, электрическими и магнитными полями, — что не отвечает требованиям представления частицы в виде волны.
При описании процессов распространения волн различают физическую и геометрическую дисперсию. Физическая дисперсия обусловлена свойствами среды, в которой распространяется волна. В этом случае фазовая скорость волны определяется приведенной выше формулой. Однако, изменение фазовой скорости с частотой возникает и при распространении в среде, которая является не дисперсионной, но область существования волны ограничена. С многочисленными примерами такой ситуации встречаемся при изучении волновых полей в волноводах. В волноводе, содержащем идеальную сжимаемую жидкость (газ) фазовая скорость нормальной волны с ростом частоты меняется от бесконечности до скорости волны в соответствующей неограниченной среде (нормальная дисперсия). Более сложные дисперсионные соотношения характеризуют свойства волн в упругих волноводах, то есть волноводах образованных идеальными упругими телами. В них возможно формирование волн, которые имеют противоположные знаки групповой и фазовой скорости[11]
Поляризация |
- Поперечная волна характеризуется нарушением симметрии распределения возмущений относительно направления её распространения (например, напряжённость электрического и магнитного полей в электромагнитных волнах).
На этом свойстве основана экспериментальная проверка поперечности световых и ЭМ волн как оптическими[12], так и радиофизическими способами[8]. В оптике это осуществляется путём последовательного пропускания луча через два поляризатора. При их скрещенном положении на выходе свет исчезает. Впервые получил обычный и необычный поляризованный свет Эразм Бартолинус в 1669 году. В радиофизике опыт проводится в УКВ-диапазоне с помощью волноводов. При скрещенных волноводах сигнал в приёмнике исчезает. Впервые этот опыт провёл П. Н. Лебедев в начале XX века.
- В продольной волне данное нарушение симметрии не возникает, так как распространение возмущения всегда совпадает с направлением распространения волны.
Взаимодействие с телами и границами раздела сред |
Если на пути волны встречается какой-либо дефект среды, тело или граница раздела двух сред, то это приводит к искажению нормального распространения волны. В результате этого наблюдаются следующие явления:
- Отражение
- Преломление
- Рассеяние
- Дифракция
- Резонанс
Конкретные эффекты, возникающие при этих процессах, зависят от свойств волны и характера препятствия.
Наложение волн |
Излучения с разной длиной волны, но одинаковые по физической природе, могут интерферировать. При этом могут возникнуть следующие частные эффекты:
стоячие волны;
бегущие волны;
биения — периодическое уменьшение и увеличение амплитуды суммарного излучения;
волновой пакет — образующиеся максимумы амплитуды имеют прерывистое распределение (волновой пакет Гаусса);
эффект Доплера — изменение частоты, воспринимаемой приёмником при движении приёмника или источника излучения.
Контролируемые биения используют для передачи информации. Существует передача информации с помощью амплитудной, частотной, фазовой и поляризационной[13] модуляции.
Конечный результат проявления от встречи волн зависит от их свойств: физической природы, когерентности, поляризации и т. д.
Математические выражения, описывающие волновые процессы |
В связи с многообразием, нелинейностью свойств субстанции, особенностями границ и способов возбуждения, пользуются свойством разложения любых, самых сложных колебаний в спектр по частотам отклика субстанции на возбуждение. Для дискретных спектров наиболее общим решением моделирующих уравнений является выражение, которое удобно представлять в комплексной форме:
u=∑j=0nAj(r,t)expi(ωjt−kjr+φj)+Bj(r,t)expi(ωjt+kjr+ψj),{displaystyle u=sum limits _{j=0}^{n}{A_{j}left({r,t}right)exp ileft({omega _{j}t-k_{j}r+varphi _{j}}right)}+B_{j}left({r,t}right)exp ileft({omega _{j}t+k_{j}r+psi _{j}}right),}

где j{displaystyle j}




Для интегральных спектров вместо сумм записываются интегралы по частотам спектра.
В дискретных структурах имеют место три режима колебательного процесса: периодический, критический, и апериодический.
В идеальной дискретной системе переход от одного режима к другому определяется разностью фаз колебания соседних элементов. При достижении противофазности колебаний система переходит от периодического режима к критическому. В апериодическом режиме противофазность колебаний соседних элементов сохраняется, но от точки возбуждения идёт интенсивное затухание колебательного процесса последующих элементов системы. Данный режим проявляется и в конечных упругих линиях.
В линиях с сопротивлением колебания соседних элементов никогда не достигают противофазности. Тем не менее, особенности колебаний, характерные для апериодического режима, сохраняются и при наличии сопротивления.
Гармоническая волна |
Гармонической волной называется линейная монохроматическая волна, распространяющаяся в бесконечной динамической системе.
В распределённых системах общий вид волны описывается выражением, являющимся аналитическим решением линейного волнового уравнения
u=Asin(ωt−kr+φ0),{displaystyle u=Asin left({omega t-kr+varphi _{0}}right),}

где A{displaystyle A}







Лучи волны |
Лучом волны (геометрическим лучом) называется нормаль к волновому фронту. Например, плоской волне (см. раздел «Классификация волн») соответствует пучок параллельных прямых лучей; сферической волне — радиально расходящийся пучок лучей.
Расчёт формы лучей при небольшой длине волны — по сравнению с препятствиями, поперечными размерами фронта волны, расстояниями до схождения волн и т. п. — позволяет упростить сложный расчёт распространения волны. Это применяется в геометрической акустике и геометрической оптике.
Наряду с понятием «геометрический луч», зачастую удобно использовать понятие «физический луч», который является линией (геометрическим лучом) только в определённом приближении, когда поперечными размерами самого луча можно пренебречь. Учёт физичности понятия луча позволяет рассматривать волновые процессы в самом луче, наряду с рассмотрением процессов распространения луча как геометрического. Особенно это важно при рассмотрении физических процессов излучения движущимся источником.
Направления исследований волн |
- Получение точных решений для различных нелинейных волн
- Распространение волн в случайных средах[источник не указан 815 дней]

Этот раздел не завершён.
См. также |
- Колебания
- Автоволны
- Электромагнитные колебания
- Волны де Бройля
- Волны на воде
- Волны-убийцы
- Поляризация волн
Примечания |
↑ 12345 Волны // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 1. — С. 315. — ISBN 5-85270-034-7.
↑ Г. Пейн, Физика колебаний и волн, стр. 161
↑ Строго говоря, это равенство справедливо только для гармоничных волн.
↑ Н. И. Калитеевский, Волновая оптика, с. 33
↑ К. А. Самойло, Радиотехнические цепи и сигналы, с. 19
↑ Л. Э. Эльсгольц, Дифференциальные уравнения и вариационное исчисление, с. 113.
↑ Н. И. Калитеевский, Волновая оптика, с. 136.
↑ 123 Н. И. Калитеевский, Волновая оптика, с. 47.
↑ Н. И. Калитеевский, волновая оптика, с. 49.
↑ Н. И. Калитеевский, волновая оптика, с. 314.
↑ Гринченко В. Т., Мелешко В. В. Гармонические колебания и волны в упругих телахю—Киев, Наукова думка, 1981.—284 с.|http://www.nehudlit.ru/books/garmonicheskie-kolebaniya-i-volny-v-uprugikh-telakh.html
↑ Р. В. Поль, Оптика и атомная физика, с. 204.
↑ К. Г. Гусев, Атлас поляризационных параметров эллиптически поляризованных волн, отражённых от сред земной поверхности, Харьков, 1966 г., тип. ХВКИУ, Г-884029
Литература |
Крауфорд Ф. Берклеевский курс физики, том 3, Волны.
Ландау Л. Д., Лифшиц Е. М. Курс теоретической физики, том 6, Гидродинамика.издание?
Уизем Дж. Линейные и нелинейные волны — М.: Мир, 1977.
Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 85—88. ISBN 5-85270-306-0 (БРЭ)
Кабисов К. С., Камалов Т. ф., Лурье В. А. Колебания и волновые процессы, Теория, задачи с решениями, URSS. 2017. 360 с. ISBN 978-5-397-05912-1.
Ссылки |
- Броунов П. И. Волны // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Физика (колебания и волны). Базовая терминология



