Rstykt

Дедеки́ндово сече́ние (или у́зкая щель) — один из способов построения вещественных чисел из рациональных.

Множество вещественных чисел определяется как множество дедекиндовых сечений.
На них возможно продолжить операции сложения и умножения.

История |

Метод был введён Дедекиндом^[1].
Это же построение неявно присутствует в «Началах» Евклида,
а именно, в книге V определение 5 звучит следующим образом:

Говорят, что величины находятся в том же отношении
первая ко второй и третья к четвёртой,
если равнократные первой и третьей
одновременно больше,
одновременно равны или
одновременно меньше
равнократных второй и четвёртой
каждая каждой при какой бы то ни было кратности,
если взять их в соответствующем порядке (9, 10, 11, 12).^[2]

Определение |

Дедекиндово сечение — это разбиение множества рациональных чисел Q{displaystyle mathbb {Q} } на два подмножества A{displaystyle A} (нижнее, или левое) и B{displaystyle B} (верхнее, или правое) такие, что:

1. 
   a<b{displaystyle a<b} для любых a∈A{displaystyle ain A} и b∈B{displaystyle bin B},


2. 
   B{displaystyle B} не имеет минимального элемента.

Примеры |

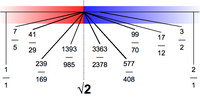
Дедекиндово сечение √2

Вещественному числу 2{displaystyle {sqrt {2}}} соответствует дедекиндово сечение, определяемое

A={x∈Q∣x⩽0∨x2<2}{displaystyle A={xin mathbb {Q} mid xleqslant 0lor x^{2}<2}} и

B={x∈Q∣x>0∧x2>2}.{displaystyle B={xin mathbb {Q} mid x>0land x^{2}>2}.}

Интуитивно можно представить себе, что для того, чтобы определить 2{displaystyle {sqrt {2}}}, мы рассекли множество на две части: все числа, что левее 2{displaystyle {sqrt {2}}}, и все числа, что правее 2{displaystyle {sqrt {2}}}; соответственно, 2{displaystyle {sqrt {2}}} равен точной нижней грани множества B{displaystyle B}.

См. также |

• Конструктивные способы определения вещественного числа

Примечания |