Rstykt

Статистическая физика

S=kBln⁡Ω{displaystyle S=k_{B},ln Omega }

Термодинамика Молекулярно-кинетическая теория

Статистики Максвелла-Больцмана Бозе-Эйнштейна · Ферми-Дирака Parastatistics · Энионная статистика Braid statistics

Ансамбли Микроканонический · Канонический Большой канонический Изотермо-изобарический Изоэнтальпи-изобарический

Термодинамика Уравнение состояния · Цикл Карно · Закон Дюлонга — Пти

Модели Модель Дебая · Эйнштейна · Модель Изинга

Потенциалы Внутренняя энергия · Энтальпия Свободная энергия Гельмгольца потенциал Гиббса · Большой термодинамический потенциал

Известные учёные Максвелл · Гиббс · Больцман

См. также: Портал:Физика

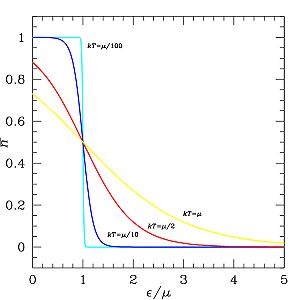
Распределение Ферми — Дирака как функция от ε/μ{displaystyle scriptstyle {varepsilon /mu }}, построенная для 4 различных температур. С ростом температуры ступенька размывается.

Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; предложена в 1926 году итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень.

Работы по статистике Ферми — Дирака были опубликованы в 1926 году, а в 1927 она была применена Арнольдом Зоммерфельдом к электронам в металле.

В статистике Ферми — Дирака среднее число частиц в состоянии с энергией εi{displaystyle varepsilon _{i}} есть

ni=giexp⁡(εi−μkT)+1,{displaystyle n_{i}={frac {g_{i}}{exp left({dfrac {varepsilon _{i}-mu }{kT}}right)+1}},}

где

ni{displaystyle n_{i}} — среднее число частиц в состоянии i{displaystyle i},

εi{displaystyle varepsilon _{i}} — энергия состояния i{displaystyle i},

gi{displaystyle g_{i}} — кратность вырождения состояния i{displaystyle i} (число состояний с энергией εi{displaystyle varepsilon _{i}}),

μ{displaystyle mu } — химический потенциал (который равен энергии Ферми EF{displaystyle E_{F}} при абсолютном нуле температуры),

k{displaystyle k} — постоянная Больцмана,

T{displaystyle T} — абсолютная температура.

В (идеальном) ферми-газе в пределе низких температур μ=EF{displaystyle mu =E_{F}}. В этом случае (полагая уровни энергии невырожденными gi=1{displaystyle g_{i}=1}), функция распределения частиц называется функцией Ферми:

F(E)=1exp⁡(εi−EFkT)+1.{displaystyle F(E)={frac {1}{exp left({dfrac {varepsilon _{i}-E_{F}}{kT}}right)+1}}.}

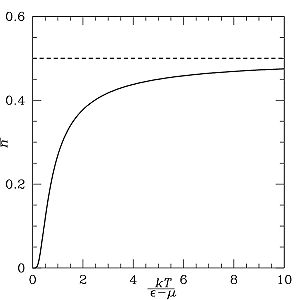
Распределение Ферми — Дирака как функция температуры. Заполнение уровней с энергиями ε>μ{displaystyle scriptstyle {varepsilon >mu }} растёт с увеличением температуры.

Применение |

Статистики Ферми — Дирака и Бозе — Эйнштейна применяются в том случае, когда необходимо учитывать квантовые эффекты, когда частицы обладают «неразличимостью». Квантовые эффекты проявляются тогда, когда концентрация частиц N/V⩾nq{displaystyle N/Vgeqslant n_{q}} (где nq{displaystyle n_{q}} — квантовая концентрация).

Квантовая концентрация — это концентрация, при которой расстояние между частицами соразмерно с длиной волны де Бройля, то есть когда волновые функции частиц соприкасаются, но не перекрываются. Квантовая концентрация зависит от температуры. Статистика Ферми — Дирака (Ф — Д) применяется к фермионам (частицы, на которые действует принцип Паули), статистика Бозе — Эйнштейна (Б — Э) применяется к бозонам. Оба этих распределения становятся распределением Максвелла — Больцмана при высоких температурах и низких концентрациях.

Распределением Максвелла — Больцмана часто описываются классические «различимые» частицы. Другими словами, конфигурация частицы A{displaystyle A} в состоянии 1 и частицы B{displaystyle B} в состоянии 2 отличается от конфигурации частицы B{displaystyle B} в состоянии 1 и частицы A{displaystyle A} в состоянии 2. Когда эта идея была проработана полностью, оказалось, что распределение частиц по энергетическим состояниям приводит к нефизическим результатам для энтропии, что известно, как парадокс Гиббса. Эта проблема исчезла, когда стал ясен тот факт, что все частицы неразличимы. И Ф — Д, и Б — Э приближаются к статистике Максвелла — Больцмана в пределе высоких температур и низких плотностей. Статистика Максвелла — Больцмана хорошо описывает поведение газов. Ф — Д часто используется для описания электронов в твердых телах, на ней, к примеру, базируются основные положения теории полупроводников в частности и электроники в целом.

Вывод распределения |

Распределение Ферми — Дирака как функция от ε{displaystyle scriptstyle {varepsilon }}. Высокоэнергетические состояния имеют меньшую вероятность. Или, низкоэнергетические состояния более вероятны.

Рассмотрим состояние частицы в системе, состоящей из множества частиц. Энергия такой частицы равна ε{displaystyle varepsilon }. Например, если наша система — это некий квантовый газ в «ящике», то подобное состояние может описываться частной волновой функцией. Известно, что для большого канонического ансамбля, функция распределения имеет вид

Z=∑se−(E(s)−μN(s))/kT,{displaystyle Z=sum _{s}e^{-(E(s)-mu N(s))/kT},}

где

E(s){displaystyle E(s)} — энергия состояния s{displaystyle s},

N(s){displaystyle N(s)} — число частиц, находящихся в состоянии s{displaystyle s},

μ{displaystyle mu } — химический потенциал,

s{displaystyle s} — это индекс, пробегающий все возможные микросостояния системы.

В данном контексте, система имеет фиксированные состояния. Итак, если какое либо состояние занято n{displaystyle n} частицами, то энергия системы — n⋅ε{displaystyle ncdot varepsilon }. Если состояние свободно, то энергия имеет значение 0. Будем рассматривать равновесные одночастичные состояния как резервуар. После того, как система и резервуар займут одно и то же физическое пространство, начинает происходить обмен частицами между двумя состояниями (фактически, это явление мы и исследуем). Отсюда становится ясно, почему используется описанная выше функция распределения, которая, через химический потенциал, учитывает поток частиц между системой и резервуаром.

Для фермионов, каждое состояние может быть либо занято одной частицей, либо свободно. Поэтому, наша система имеет два множества: занятых (разумеется, одной частицей) и незанятых состояний, обозначающихся s1{displaystyle s_{1}} и s2{displaystyle s_{2}} соответственно. Видно, что E(s1)=ε{displaystyle E(s_{1})=varepsilon }, N(s1)=1{displaystyle N(s_{1})=1}, и E(s2)=0{displaystyle E(s_{2})=0}, N(s2)=0{displaystyle N(s_{2})=0}. Поэтому функция распределения принимает вид:

Z=∑i=12e−(E(si)−μN(si))/kT=e−(ε−μ)/kT+1.{displaystyle Z=sum _{i=1}^{2}e^{-(E(s_{i})-mu N(s_{i}))/kT}=e^{-(varepsilon -mu )/kT}+1.}

Для большого канонического ансамбля, вероятность того, что система находится в микросостоянии sα{displaystyle s_{alpha }} вычисляется по формуле

P(sα)=e−(E(sα)−μN(sα))/kTZ.{displaystyle P(s_{alpha })={frac {e^{-(E(s_{alpha })-mu N(s_{alpha }))/kT}}{Z}}.}

Наличие состояния, занятого частицей, означает, что система находится в микросостоянии s1{displaystyle s_{1}}, вероятность которого

n¯=P(s1)=e−(E(s1)−μN(s1))/kTZ=e−(ε−μ)/kTe−(ε−μ)/kT+1=1e(ε−μ)/kT+1.{displaystyle {bar {n}}=P(s_{1})={frac {e^{-(E(s_{1})-mu N(s_{1}))/kT}}{Z}}={frac {e^{-(varepsilon -mu )/kT}}{e^{-(varepsilon -mu )/kT}+1}}={frac {1}{e^{(varepsilon -mu )/kT}+1}}.}

n¯{displaystyle {bar {n}}} называется распределением Ферми — Дирака. Для фиксированной температуры T{displaystyle T}, n¯(ε){displaystyle {bar {n}}(varepsilon )} есть вероятность того, что состояние с энергией ε{displaystyle varepsilon } будет занято фермионом. Обратите внимание, что
n¯{displaystyle {bar {n}}} является убывающей функцией от ε{displaystyle varepsilon }. Это соответствует нашим ожиданиям: высокоэнергетические состояния занимаются с меньшей вероятностью.

Обратите внимание, что энергетический уровень ε{displaystyle varepsilon } имеет вырождение gε{displaystyle g_{varepsilon }}. Теперь можно произвести простую модификацию:

n¯=gε⋅1e(ε−μ)/kT+1.{displaystyle {bar {n}}=g_{varepsilon }cdot {frac {1}{e^{(varepsilon -mu )/kT}+1}}.}

Это число — ожидаемое число частиц, в суммарном состоянии с энергией ε{displaystyle varepsilon }.

Для всех температур T{displaystyle T}, n¯(μ)=12{displaystyle {bar {n}}(mu )={frac {1}{2}}}. Это означает, что состояния с энергией μ{displaystyle mu } всегда будут иметь одинаковую вероятность быть заполненными или свободными.

В пределе T→0{displaystyle Tto 0}, n¯{displaystyle {bar {n}}} становится ступенчатой функцией (см. первый график). Все состояния с энергией меньше химического потенциала μ{displaystyle mu } будут заняты с вероятностью 1. Состояния с энергией выше химического потенциала μ{displaystyle mu } будут свободны. Химический потенциал при нулевой температуре — энергия Ферми, обозначается EF{displaystyle E_{F}}, то есть
EF=μ(T=0).{displaystyle E_{F}=mu (T=0).}

Влияние температуры |

Необходимо заметить, что химический потенциал зависит от температуры. Однако для систем, имеющих температуру ниже температуры Ферми TF=EFkB{displaystyle T_{F}={frac {E_{F}}{k_{B}}}}, что часто используется, как аппроксимация, μ≈EF{displaystyle mu approx E_{F}}.
В реальности же:

μ=EF∑n=0,1,2…[(−1)nπ2n22n(2n+1)(kBTEF)2n]=EF[1−π212(kBTEF)2+π480(kBTEF)4+…].{displaystyle mu =E_{F}sum _{n=0,1,2dots }{left[(-1)^{n}{frac {pi ^{2n}}{2^{2n}(2n+1)}}left({frac {k_{B}T}{E_{F}}}right)^{2n}right]}=E_{F}left[1-{frac {pi ^{2}}{12}}left({frac {k_{B}T}{E_{F}}}right)^{2}+{frac {pi ^{4}}{80}}left({frac {k_{B}T}{E_{F}}}right)^{4}+ldots right].}

Другой вывод |

См. также |

• Интеграл Ферми-Дирака


• Статистика Бозе — Эйнштейна


• Статистика Максвелла — Больцмана


• Распределение Максвелла


• Закон Видемана — Франца